The Conjugate Prior: A Prior Distribution That Simplifies the Calculation of the Posterior Distribution

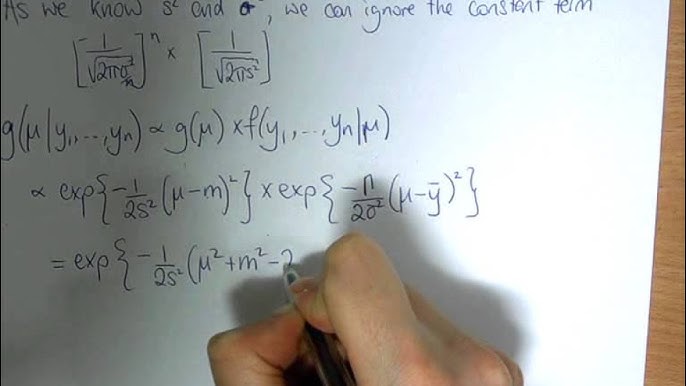
In the grand theatre of statistics, Bayesian inference plays the role of a wise alchemist — transforming data into understanding through the delicate balance of belief and evidence. Yet, within this process lies a mathematical hurdle: updating beliefs (priors) in light of new data to obtain a refined belief (posterior). The calculations can grow tangled, but one elegant concept — the Conjugate Prior — enters like a master key, unlocking simplicity amidst complexity.

1. The Bayesian Story: A Tale of Beliefs and Evidence

Imagine you’re a chef experimenting with a new recipe. Before tasting, you already have a belief — say, that your dish will be delicious. This belief is your prior. Then you take a bite — the data — and update your opinion based on what you tasted. That updated opinion? It’s your posterior belief.

Bayesian statistics works exactly like that — continuously refining our beliefs as new evidence appears. However, when data grows complex, updating these beliefs mathematically can become cumbersome. The Conjugate Prior simplifies this beautifully by ensuring that the updated belief (posterior) has the same functional form as the original prior.

For students exploring probability theory in a data science course in Mumbai, understanding this concept is a game-changer. It demonstrates how prior assumptions can be woven neatly into computational frameworks without getting lost in mathematical chaos.

2. The Magic of Mathematical Harmony

The idea of a conjugate prior is rooted in mathematical elegance. Suppose your data follows a particular likelihood — say, a Binomial distribution. By choosing a prior that belongs to the Beta family, you can ensure the posterior remains Beta as well. This relationship between the likelihood and the prior — where both “speak the same language” — is what makes them conjugate.

Think of it like tuning two musical instruments to the same key. When they’re in harmony, the resulting melody — your posterior — resonates smoothly. This harmony eliminates the need for complex integration or simulation, allowing statisticians and data scientists to compute results efficiently.

Many aspiring analysts who enroll in a data scientist course often find this concept illuminating because it bridges theory and practicality. It shows how smart choices in modeling can dramatically reduce computational burden while retaining interpretability.

3. The Conjugate Families: Partnerships in Probability

Conjugate priors are not a single entity but a family of beautifully paired distributions. Here are a few classical partnerships:

• Beta-Binomial Pair: For binary outcomes (success/failure), the Beta prior conjugates perfectly with the Binomial likelihood.
• Gamma-Poisson Pair: When modeling count data, the Gamma prior complements the Poisson likelihood seamlessly.
• Normal-Normal Pair: For continuous data with known variance, the Normal distribution acts as its own conjugate.

Each pair tells a story of balance — of beliefs that evolve gracefully without distorting their original form. This consistency allows statisticians to work faster, particularly in iterative or real-time systems where data continuously streams in.

If you’re taking a data science course in Mumbai, these conjugate relationships offer a powerful toolkit for practical Bayesian modeling — whether for spam filtering, disease prediction, or market forecasting.

4. Why Conjugate Priors Still Matter in the Age of Big Data

In an era dominated by machine learning and neural networks, one might wonder if conjugate priors have become relics of the past. On the contrary, they remain vital for interpretability, speed, and conceptual clarity.

In domains like A/B testing, reliability modeling, and even reinforcement learning, conjugate priors serve as efficient shortcuts — reducing computational cost while preserving statistical rigor. Their analytical nature allows decision-makers to obtain closed-form posteriors, which are far easier to explain than black-box models.

Professionals who complete a data scientist course often rediscover these classical Bayesian ideas while working on modern AI applications. They find that the simplicity and transparency of conjugate priors often outperform complex algorithms when data is limited or interpretability is essential.

5. Beyond Simplicity: The Philosophy of Conjugacy

At its heart, the conjugate prior represents more than just computational efficiency — it embodies the philosophy of alignment. In life and learning, when your prior beliefs align with the nature of the evidence, understanding unfolds effortlessly. Conjugate priors remind us that elegant solutions often come not from complexity, but from choosing harmony over discord.

For data enthusiasts, the concept is both mathematical and metaphorical — a testament to how thoughtful assumptions can lead to profound clarity. Whether you’re exploring Bayesian reasoning or diving deeper into inferential statistics, conjugate priors stand as a bridge between belief and evidence, simplicity and precision.

Conclusion: A Symphony of Belief and Evidence

The Conjugate Prior is more than a mathematical trick — it’s a symphony where prior beliefs and data play in perfect rhythm. It transforms the arduous task of updating probabilities into an intuitive and elegant process.

For anyone pursuing a data science course in Mumbai, mastering conjugate priors means learning to think like a Bayesian — blending logic, intuition, and mathematics into one cohesive narrative. And for every data practitioner, it’s a reminder that in the complex orchestra of uncertainty, harmony often lies in the simplest of relationships.

Business name: ExcelR- Data Science, Data Analytics, Business Analytics Course Training Mumbai

Address: 304, 3rd Floor, Pratibha Building. Three Petrol pump, Lal Bahadur Shastri Rd, opposite Manas Tower, Pakhdi, Thane West, Thane, Maharashtra 400602

Phone: 09108238354 

Email: enquiry@excelr.com